
運用目標が決まれば、それを実現するためのプロセス(運用戦略)を考えることが出来ます。
ここまでに①運用資金、②目標利回り、③許容DDの3つを明確化しましたが、この状態では未だ運用戦略を検討する上では不十分です。
次に実施すべきことは、運用目標をストラテジー(=売買ルール)に求められる要件に落とし込むことです。
これは、運用目標を達成するためにどのようなパフォーマンスを有するストラテジーが必要か、明確にする行為です。
更に例えると、あなたが市販のストラテジーを購入しようとした際、何を基準として購入可否を判断するか、ということです。
ストラテジーへの要件が明らかになれば、必然的に対象市場や運用期間、順張りや逆張りなどの運用戦略が決まってきます。
1.ストラテジーの評価指標
ストラテジーを評価する指標として、勝率、プロフィットファクター、シャープレシオ、ペイオフレシオなどがあります。
どのような指標でストラテジーの良否を判断すればよいでしょうか。
(1)プロフィットファクター(P/F)
ストラテジーを評価する指標で有名なものはプロフィットファクターです。
P/Fの定義は総利益÷総損失であり、単位当たりの損失に対してどれくらいの利益が得られるかを表わす指標です。
感覚的にも理解しやすい指標だと思います。
市販のストラテジーには「P/Fが2を超える」などの謳い文句をよく見かけます。
しかし、P/Fは収益性を判断する上ではあまり役に立ちません。
運用目標でも触れたとおり、資産運用にとって重要なファクターはリターンとリスクです。
P/Fでの評価は、どれだけ儲けがあってどれだけ損をしたか振り返る行為です。
結果のみに着目しており、その過程でどれだけリスクが発生したか分かりません。
「総損失がリスクを表わしている」と考える方がいるかもしれませんが、損失はマイナスの収益(期待値)であり、リスク(不確実性)ではないのです。
(2)シャープレシオ(S/R)
ではシャープレシオはどうでしょうか。
シャープレシオ(以下S/R)はリターンの母集団に対する期待値/標準偏差であり、単位当たりのリスクに対してどれだけの利益が期待できるかを表わす指標です。
リスク調整済みリターンとも呼ばれます。
S/Rは非常に有用な指標であり、ファンドの成績を定量化するのにも使われます。
ただし、シストレ上はS/R単独での収益性予測はできません。
例えば、「シャープレシオが0.2のストラテジーで年利30%となるよう運用してください」と言われても検討することができないのです。
2.ストラテジーへの要件
結論として、収益性の予測には下記の3つが必要です。
①リターンの期待値
②リターンの標準偏差
③トレード数
シャープレシオは上記の①÷②ですが、資産運用においてはそれぞれを独立して把握しておく必要があります。
どれも重要なファクターですが、この中でも特に重要なファクターが「トレード数」と考えています。
(1)トレード数が与える効用
あるストラテジーについて、①リターンの期待値、②リターンの標準偏差、③トレード数を用いて収益性を予測します。
リターンの母集団の期待値をe、標準偏差をσ、単位期間(例えば1年当たり)のトレード数をNとし、このストラテジーで単位期間運用したときの総利益について、その期待値Eと標準偏差Σを考えます。
(a)運用期間が経過した時点での総利益の期待値
この計算は簡単です。
1回当たりのトレードの期待値がeでN回トレードをするため、運用期間通しての総利益の期待値は下記の通りです。
E=N×e
(b)運用期間が経過した時点での総利益の標準偏差
こちらは少し難しくなります。
まず母集団1(e1,σ1)と母集団2(e2,σ2)の合成標準偏差σ12を考えます。
σ12は下記の式で与えられます。
σ12=SQRT(σ1^2+2×r12×σ1×σ2+σ2^2)
ここでr12は母集団1と母集団2の相関係数です。
さて、ここで母集団1を1回目のトレード、母集団2を2回目のトレードと考えます。
母集団1、2は、同じ母集団から抽出されたサンプルのため、σ1=σ2=σです。
また、1回目のトレードと2回目のトレードの間には相関がないとします。
従って、r12=0とおくと、
σ12=SQRT(σ^2+σ^2)=SQRT(2)×σ
となり、2回のトレード経過後における収益の標準偏差は、1回のトレードによる標準偏差σにSQRT(2)を掛けたものになります。
上記で計算したのは2回のトレードにおける合成標準偏差ですが、
これをN回のトレードに一般化すると下記となります。
Σ=SQRT(N)×σ
※注意しておきたいのは、1回目と2回目のトレードの間に相関がある場合です。この場合、r12≠0となるため上記の式は当てはまりません。これは例えば「1回目に勝てば2回目も勝ちやすい」などの癖があるトレードです。
つまり、運用期間を経た時点でのシャープレシオSR’は以下となります。
SR’=E/Σ=SQRT(N)×(e/σ)=SQRT(N)×(SR)
この式で理解できると思いますが、シャープレシオが同じ場合でもトレード数が多いストラテジーを単位期間運用した場合、見掛け上シャープレシオが改善する(収益性が向上する)ことに気付きます。
これが「トレード数が資産運用に与える定量的な効果」となります。
(2)ストラテジーへの要件と運用レシオ
さて、前回までに導出した変数を用いて、ストラテジーを単位期間運用した場合の資産曲線を表すと次のような形となります。
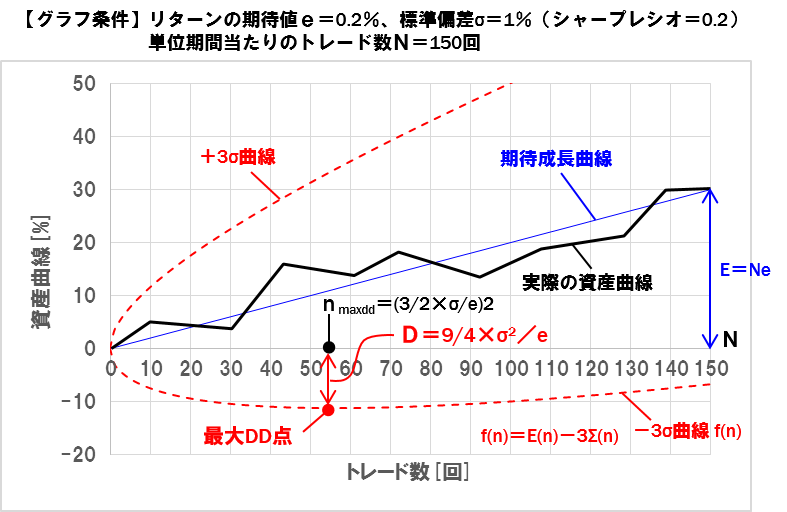
資産の曲線の上下に引かれているラインは、それぞれ+3σと-3σのラインです。
運用中の資産曲線がこのラインに触れる確率は0.3%です。
この資産曲線を用いて、運用目標で定めた目標利回りと許容DDからストラテジーへの必要要件を明確化します。
図において、初期資金に対する最大ドローダウン(以下D)は、-3σ曲線が極値を取るポイントとなります。
トレード数nに対する-3σ曲線の式f(n)は以下となります。
f(n)=E(n)-3Σ(n)=n×e-3×SQRT(n)×σ
この値を微分し、f’(n)=0としてnについて解くと、
f’(n)=e-3/2×N^(-1/2)×σ=0
n=(3/2×σ/e)^2=(3/2×(1/SR))^2 (=n_maxdd)
このストラテジーにおいて、上記のトレード数n_maxddのときに下記の最大ドローダウンDが0.3%の確率で発生する可能性があります。
初期資金からだけでなく、どの時点の資金から見てもこの値となります。
D=9/4×σ^2/e
ストラテジーは当初取り決めた目標利回りと許容DDに対し、以下の2つの式を満足する必要があります。
E≧目標利回り,D≦許容DD
この2つの式をまとめると下記のようになります。
E/D≧目標利回り/許容DD
ここで右辺の目標利回り/許容DDを、運用レシオAと仮に呼ぶことにします。
この式をストラテジーの元の指標であるe,σ,Nで表すと、以下のようになります。
この式が運用目標に対するストラテジーの必要要件を表す式となります。
4/9×N×(e/σ)^2≧A
左辺のe/σはシャープレシオですのでトレード数とシャープレシオのみでも計算可能です。
最大DDの計算や手数料の影響など詳細検討の上でeとσは独立して必要となります。
シストレ売買サイトで販売されているストラテジーの主流は、シャープレシオ0.2、年間トレード数200回程度です。
上記の左辺を計算すると3.55となるため、このストラテジーを用いた場合、年利35.5%、許容DD10%(発生確率0.3%)を達成することができます。
独自のストラテジーを所有している方は計算してみると良いかと思います。
(3) 元本の保証
最後にトレード数を拡張した場合の資産曲線を見てみます。
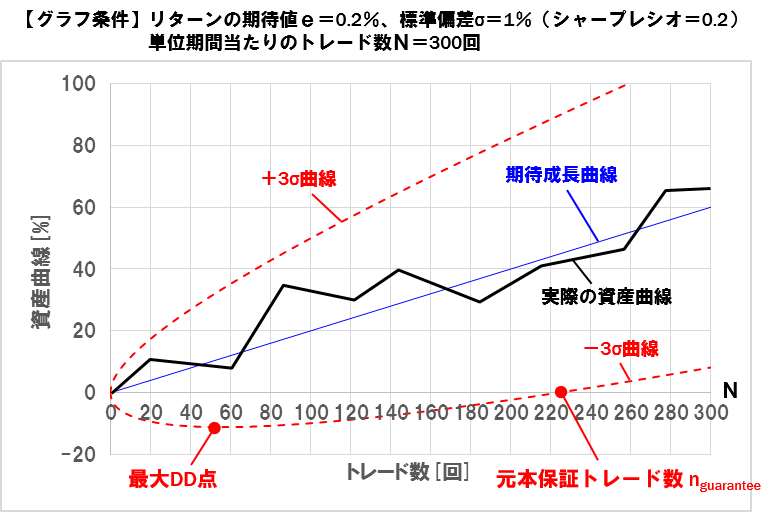
この曲線を見ると、運用期間が経過した時点で-3σ曲線が0より大きくなります。
-3σ曲線が0以上となるトレード回数は、
n_guarantee=9×(σ/e)^2
であり、このトレード数を上回ると99.7%の確率で元本を保証することができます。
冒頭で「トレード数が重要」と述べたのは、この理由からです。
運用上は年利も重視されますので、できれば1年当たりでこの数値を上回る程度のトレード数は確保しておきたいものです。
このように運用目標からストラテジーの要件への落とし込みが完了したので、所望の値を満足すべくe、σ、Nを設計することになります。
e,σ,Nは互いに絡み合うため一意的な設計はできませんが、どのように設計していけばよいか次回からその考え方に個別に触れていきたいと思います。