「An Improved Pairs Trading Strategy based on Switching Regime Volatility」
(Marco Bee, Giulio Gatti, 2015/7/27)
2つの商品・株式インデックスのペアトレードに関する論文です。タイトル的にはレジームスイッチがメインに見えますが、ここで取り上げたのは別の理由からです。
ペアトレード、いわゆる「鞘取り」は、個別銘柄取引では鉄鋼株などでよく行われる手法です。2つの銘柄の価格の鞘の開き具合、閉じ具合を見て、割安株をロングし割高株をショートします。鞘取りで重要なことは、当然ですが以下の2点です。
(1)ペアとなる銘柄をどうやって選定するか
(2)どのようなスプレッドの水準で仕掛けるか
ここで経験的・感覚的に、
(1)鉄鋼やメガバンクなどの同業種の2銘柄で相関の高いものを候補として選定する。
(2)2つの商品(銘柄)の価格の差分にボリンジャーバンドを当てはめて特定の水準で逆張りする。
などの手法が主流となっています。しかし上記の手法は「相関が高い→鞘を埋める」という因果性があることが前提であり、当然ながらそのような統計的保証は全くありません。
ヘッジファンドや金融機関では常識として広まっていますが、ペアトレーディングの銘柄選定には「共和分検定」が使われます。この手法を用いると、少なくともバックデータから「統計的に鞘を埋める保証」が存在することになり、すなわち「鞘取り」でなく「統計的アービトラージ」と呼ぶことができます。
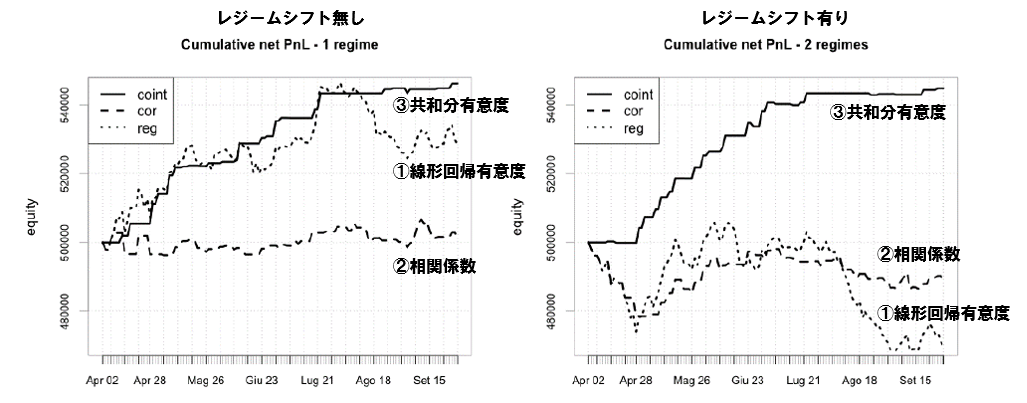
この論文では、各商品・株式インデックスペアについて、①線形回帰有意度、②相関係数、③共和分有意度の3つのフィルタを用いてペアトレードした場合の累積リターンが記載されています。この結果を見ると、③共和分有意度が優れていることが分かります。共和分検定の有効性が良く分かる論文の1つです。
なお共和分検定は、2つの銘柄の線形回帰の残差系列に単位根検定(ADF検定やPP検定)を行います。残差系列が単位根と判断された場合、残差系列には「平均回帰性」が統計的に保証されます。
y(t)=ax(t)+ε(t)において、残差系列のε(t)が「平均回帰性」を持つとき、当然ですが式を変形させて、y(t)-ax(t)も「平均回帰性」を持つことになります。y(t)-ax(t)はスプレッドの式そのものであり、すなわち「鞘が閉じる(平均に回帰する)」ことが統計的に保証されていることになります。
またこのことから分かるように、2つの変数のスプレッドの計算は、単純に比率を掛けたり足したり引いたりするのでなく、回帰係数aを用いることで統計的な意味が生まれるのです。
難しそうに聞こえる「共和分検定」ですが、R言語を使えばデータのインポート後、わずか1行でできてしまいます。
> 共和分検定P値 <- pp="" test="" lm="" data_y="" data_x="" residuals="" p="" value="" p="">